In Black–Scholes option pricing model, the implied volatility or ‘IV’ of an option contract is the cost embedded in the option of the volatility of the underlying instrument that it is being valued against. Volatility is the input in an option pricing model that measures when an asset will likely return to a theoretical value equal to the current market price of the option strike price.
Implied volatility is a future looking and subjective measurement that is different from the historical volatility of an asset. This is because the historical volatility is calculated from known past returns of a stock, commodity, or market. An option trader must understand where the implied volatility is in terms of the underlying asset, implied volatility rank is a tool used to understand an options implied volatility from a one year high and low implied volatility.
If the implied volatility range is 30 to 60 over the past year. The lowest implied volatility value is 30, and the highest implied volatility value is 60. Compare the current implied volatility value to this range to try to see how the current implied volatility ranks related to its historical implied volatility range. If the current implied volatility value is 45, then this would equal an implied volatility rank of 50% since it is in the middle of this range
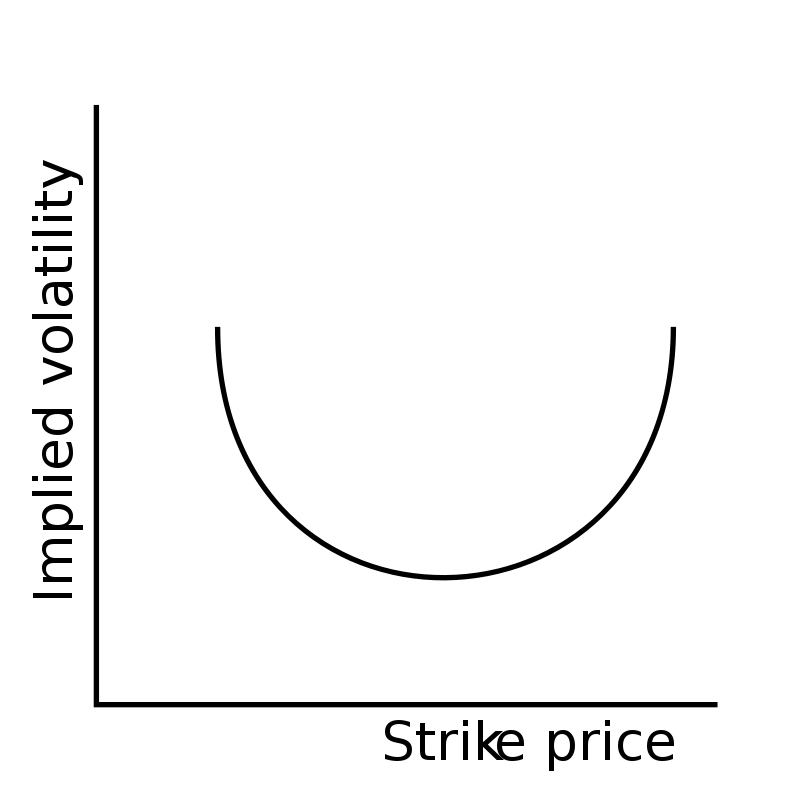
The below image is an example of a ‘volatility smile’ and can be created by implied volatility patterns that form in the prices of option chains. This curving pattern is correlated to the implied volatility in a market that is needed to modify the Black–Scholes options pricing formula to fit market prices. Options that have strike prices that differ a large amount from the underlying asset’s current price can have much greater prices due to their higher implied volatilities than what would be priced into normal option pricing models. Options with higher prices in relation to at-the-money options are called either deep in-the-money or out-of-the-money. They options have either very high delta (in-the-money) they gain intrinsic value fast or they have very low delta (out-of-the-money) and can grow in price in percentage terms due to gamma with the fast delta expansion, either of these factors make them more expensive based on their implied volatility.
I have created the Options 101 eCourse for a shortcut to learning how to trade options.