Warren Buffett’s legendary investment success stems from his disciplined application of mathematical principles to stock market investing. While he famously stated that complex math isn’t necessary for successful investing, his wealth-building strategy consistently relies on simple fundamental mathematical concepts that provide a systematic framework for evaluating opportunities and managing risk. Here are the ten math rules that made Warren Buffett a billionaire.
1. The Compound Interest Formula
Buffett discovered the power of compound interest early in life, understanding that time transforms modest investments into extraordinary wealth through the mathematical formula A = P(1 + r/n)^nt. This equation demonstrates how principal amount, interest rate, compounding frequency, and time grow exponentially. Buffett has called compound interest the eighth wonder of the world, emphasizing that starting early maximizes the time component in the equation.
The mathematical beauty of compounding lies in earning returns not just on your original investment, but on all previously accumulated gains. A $10,000 investment earning 10% annually becomes $11,000 after one year, but the second year’s 10% return applies to the full $11,000, creating $12,100.
Over the decades, this accelerating effect has become dramatic, which explains Buffett’s preference for buying and holding quality companies for extended periods rather than frequent trading. This rule applies to compounding capital gains and reinvested dividends, which Buffett has optimized.
2. The 50% Loss Equals 100% Gain Recovery Rule
Buffett’s famous principle, “Never lose money,” stems from the mathematical asymmetry of losses and gains. When an investment loses 50% of its value, it needs a 100% gain to break even. This mathematical reality becomes more severe with larger losses: a 75% decline requires a 300% gain for recovery, while a 90% loss demands a 900% gain.
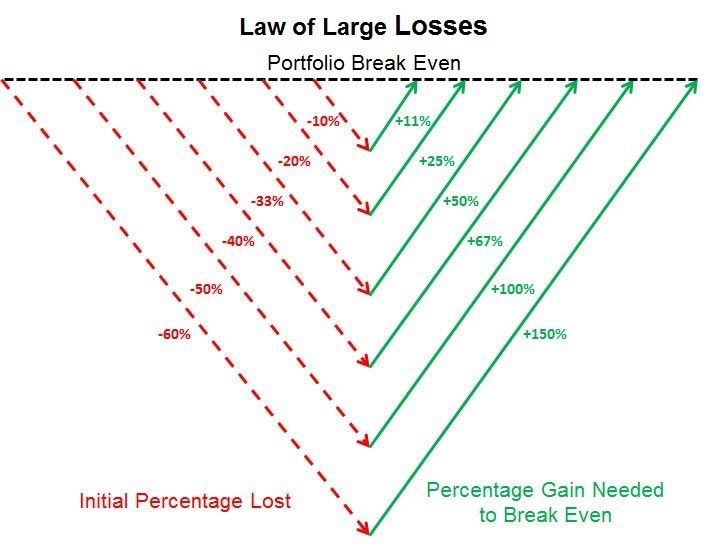
This mathematical disadvantage explains Buffett’s conservative approach to risk management. Rather than chasing high-risk, high-reward opportunities, he focuses on preserving capital by investing in companies with predictable earnings and substantial competitive advantages.
The mathematics clearly show that avoiding significant losses contributes more to long-term wealth creation than occasionally hitting home runs while suffering substantial setbacks.
3. The Discounted Cash Flow Rule
Buffett determines intrinsic value by calculating the present value of a company’s future cash flows using discounted cash flow analysis. The formula IV = Σ(CFt / (1 + r)^t) represents the sum of all future cash flows divided by one plus the discount rate raised to the power of periods. This mathematical approach values companies based on their ability to generate cash for shareholders rather than market sentiment or speculation.
Buffett defines “owner’s earnings” as net income plus depreciation and amortization, minus capital expenditures and additional working capital requirements. This calculation provides a more accurate picture of cash available to shareholders. By comparing this intrinsic value to the current market price, Buffett identifies undervalued opportunities where the mathematical analysis suggests the stock trades below its fundamental value.
4. The Opportunity Cost Optimization Rule
Every investment decision involves opportunity cost – the return foregone by choosing one investment over alternatives. Buffett applies mathematical thinking by constantly comparing potential returns across different opportunities, even in unrelated industries. This optimization process requires evaluating risk-adjusted returns to allocate capital to the most attractive opportunities.
Buffett’s approach involves creating mental hurdle rates that investments must exceed to be considered. When evaluating a potential stock purchase, he compares its expected returns to bonds, other stocks, and keeping cash. This mathematical framework ensures capital flows toward opportunities offering the best risk-adjusted returns rather than simply the most familiar or convenient options.
5. The 5/25 Concentration Rule
Buffett advocates concentrating investments in your best ideas rather than diversifying across many mediocre opportunities. His approach involves listing potential investments, identifying the top five most attractive options, and focusing exclusively on those while avoiding the temptation to pursue the remaining twenty. This mathematical approach to portfolio construction recognizes that diversification can dilute returns when applied excessively.
The mathematics of concentration works because exceptional companies generate outsized returns that average performers can’t match. At the same time, diversification reduces volatility but limits upside potential when you genuinely believe in superior opportunities. Buffett’s concentrated approach requires thorough analysis but allows mathematical compounding to work on your best ideas rather than being diluted across numerous average investments.
6. The Return on Equity Rule
Return on Equity measures how efficiently a company generates profits from shareholder equity: ROE = Net Income ÷ Shareholder Equity. Buffett seeks companies with consistently high ROE, which indicates management’s ability to create value from invested capital. This mathematical metric reveals how effectively companies deploy shareholder money to generate earnings.
Companies with sustainable high ROE possess competitive advantages that allow them to earn superior returns on invested capital. These businesses often require minimal additional investment to grow, allowing them to compound shareholder wealth efficiently.
Buffett’s focus on ROE reflects his mathematical understanding that businesses generating high returns on equity create more value than those requiring constant capital infusions to maintain growth.
7. The Margin of Safety Rule
Buffett only purchases stocks when they trade significantly below the calculated intrinsic value, creating a margin of safety that is expressed as intrinsic value minus market price. This mathematical buffer protects against analytical errors, unforeseen circumstances, and market volatility. The larger the margin, the greater the protection against permanent capital loss.
This principle, inherited from Benjamin Graham, recognizes that investment analysis involves estimates and assumptions that may prove incorrect. Buffett reduces the probability of significant losses while increasing potential returns by requiring a substantial mathematical cushion between intrinsic value and purchase price. The margin of safety transforms investing from speculation into a mathematical exercise with favorable odds.
8. The Numerical Comparison Rule
Buffett develops numerical literacy by constantly analyzing financial statements and building a mental database of business metrics. This quantitative approach allows rapid comparison of investment opportunities by quickly assessing key ratios, growth rates, and financial characteristics. The mathematical framework becomes second nature through repetitive analysis of hundreds of companies.
This numerical fluency enables pattern recognition across industries and periods. Buffett can immediately compare its financial metrics to similar companies and historical precedents when evaluating a potential investment. This mathematical approach transforms complex business analysis into a systematic comparison of quantifiable factors that indicate long-term investment attractiveness.
9. The High Probability Rule
Buffett focuses on high-probability investment scenarios rather than attempting to predict uncertain outcomes. This mathematical approach recognizes that perfect information is impossible, but some situations offer significantly better odds of success than others. He improves the mathematical probability of favorable outcomes by concentrating on predictable businesses with durable competitive advantages.
The mathematics of probability works in investing because many small advantages compound over time into significant outperformance. Rather than requiring certainty about specific outcomes, this approach seeks situations where multiple factors suggest favorable odds. Consistent application of this probability-based thinking creates a mathematical edges that accumulate into substantial wealth over decades.
10. The Mathematical Edge Rule
Buffett only makes investments when mathematical analysis suggests a favorable expected outcome. This edge might be perhaps a 55% probability of success versus a 45% probability of loss, but when applied consistently across many decisions, small mathematical advantages compound into significant outperformance. The key lies in having genuine analytical advantages rather than relying on luck or speculation.
This mathematical edge emerges from superior analysis, longer time horizons, and emotional discipline during market volatility. While individual investments may not always succeed, the mathematical law of large numbers ensures that consistent application of slight edges produces superior long-term results. Buffett’s success demonstrates how mathematical thinking applied to investing creates sustainable competitive advantages.
Conclusion
Warren Buffett’s extraordinary wealth results from consistently applying mathematical principles to investment decisions. These rules demonstrate that successful investing requires quantitative analysis, probabilistic thinking, and mathematical discipline rather than complex formulas or market timing based on predictions and opinions.
By understanding and applying these mathematical concepts, investors can build wealth through the same systematic approach that created one of history’s greatest fortunes.
