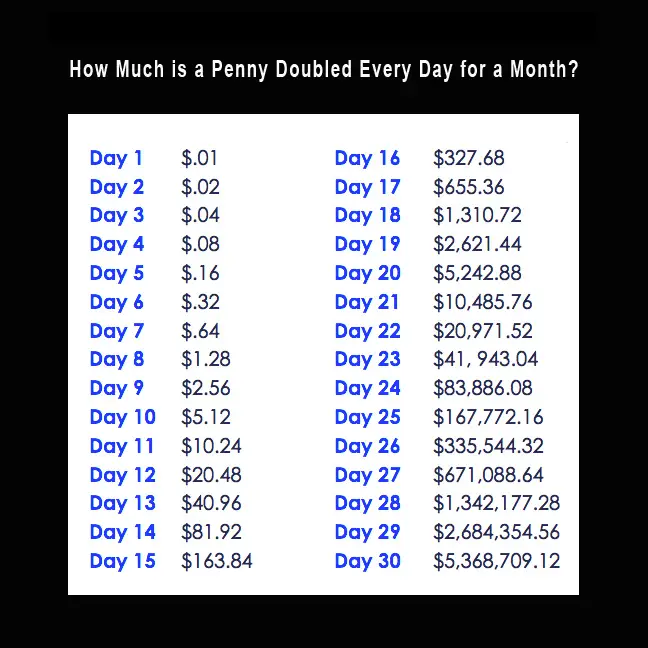
A penny doubled every day for a month is $5,368,709.12 after 30 days.
The concept of doubling a penny every day may seem simple, but it demonstrates the powerful principle of exponential growth. The idea is to start with a penny and double it every day for a month, which leads to a surprising final amount. This means on day one; you start with one cent; on day two, it doubles to two cents; on day three, you have four cents; on day four, you have eight cents, etc. In this post, we will delve into the mathematics behind the concept, break down the results of doubling a penny every day for a month and explore the real-world applications of this strategy.
The Mathematics of Doubling a Penny Every Day
Exponential growth is a mathematical concept that describes the rate at which a value increases over time. It’s characterized by a constant growth rate, often represented by a base number raised to power. In the case of doubling a penny every day for a month, the base number is 2, and the power represents the number of days.
To understand this concept better, let’s take a look at an example: If you start with a penny and double it every day for a week, the amount of money you would have at the end of the week would be $0.01, $0.02, $0.04, $0.08, $0.16, $0.32, $0.64. As you can see, the amount of money increases rapidly as the days progress. This is the essence of exponential growth.
Compounding Interest
Understanding the significance of compounding interest or compounded returns in exponential growth is also essential. Compounding interest is the interest earned on the initial investment and any interest earned on any previous interest. In the penny-doubling scenario, the interest earned on the previous day’s amount is added to the initial investment, which leads to a rapid increase in the final amount. This can also be thought of as the principle of compounding gains, as the returns on capital create new returns on the gains and grow exponentially.
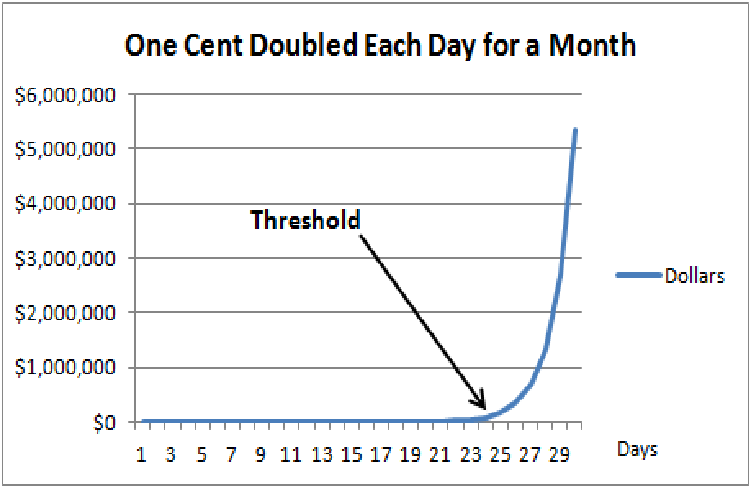
If you start with a penny and double it every day for a month, the final amount would be $5,368,709.12 if it had 30 days. Without the compounding effect, the final amount would only be $0.30 if addition was used instead of two times multiplication on the penny. Compounding returns dramatically increase the final amount, which is why exponential growth can be robust when saving and investing money for compounded capital gains.
The Real-World Applications of Penny Doubling
The scenario of doubling a penny every day for a month is a valuable tool for illustrating the power of exponential growth and compounding interest. However, it’s important to note that this scenario is purely hypothetical and doesn’t consider real-world scenarios such as taxes, inflation, and other factors that could affect the final amount of money. Also, doubling money in a short amount of time is unrealistic and used for illustrative purposes only. 10% annual return on money is a more realistic goal that will also lead to long-term compounding.
Despite this, real-world applications of compounding capital gains can be applied to investing money at a much slower rate of return. One of the most prominent applications is the power of compound gains on long-term stock market investments during bull markets as prices rise and dividends are reinvested to buy more shares. Regularly contributing to investment and allowing the capital gains to compound over time can lead to a significant amount of money accumulated over the long term. Trading systems can also create returns that can be left in the account to grow and compound over time.
Another real-world application of the penny-doubling concept is the exponential growth and compounding effect that can also be applied to businesses’ growth and marketing strategies, where small, consistent efforts can lead to significant growth over time.
For example, a business that focuses on consistently acquiring a small number of new customers daily can see significant growth over time, just like the penny-doubling scenario. Similarly, a marketing strategy focusing on consistently reaching a small number of potential customers daily can lead to significant growth and success over time.
In conclusion, a penny-doubling scenario is a valuable tool for illustrating the power of exponential growth and compounding returns. However, it’s important to note that this scenario is purely hypothetical and doesn’t consider real-world performance. Nevertheless, the penny doubling concept has real-world applications in trading, investing, and business sales and profits, where small, consistent efforts can lead to significant growth over time.
A Compounding Folktale
One Grain of Rice is a mathematical folktale found in a children’s book written and illustrated by Demi. The story is set in a village where the ruler, a clever and greedy raja, taxes the villagers heavily. The clever village girl Rani comes up with a plan to outsmart the raja by begging him to double the rice she receives for 30 days, starting with one grain on the first day. The raja agrees, not realizing that the request will eventually lead to more rice than he can provide. As the days go by, the rice Rani receives increases exponentially. On the second day, she receives two grains; on the third day, four grains, and so on. By the 30th day, Rani receives over 5.3 million grains of rice, more than the raja can provide.
The story teaches the concept of exponential growth and the power of tiny changes over time. It shows that small changes can significantly impact when given enough time. This is a mathematical concept known as compounding, the idea that the return gains on an investment are added to the principal. Then interest is earned on the new balance.
Conclusion
To sum up, the mathematical concept of exponential growth on compounding is at the heart of the penny-doubling scenario. It’s characterized by a constant growth rate represented by a base number raised powerfully over time. The significance of compounding returns in the penny-doubling scenario is that it leads to a rapid increase in the final amount, which is why exponential growth can be so robust when saving and investing money.
